Setting Up the ITK Switchboard
The Ensemble ITK Switchboard is a data-driven integration solution that allows ITK-compliant systems to interoperate with a minimum of integration work. This chapter discusses the following topics:
For additional details, see the classes in the EnsLib.ITK packages of the InterSystems Class Reference.
Overview
The Ensemble ITK Switchboard is a specialized Ensemble production that routes messages. The following figure shows its basic architecture:
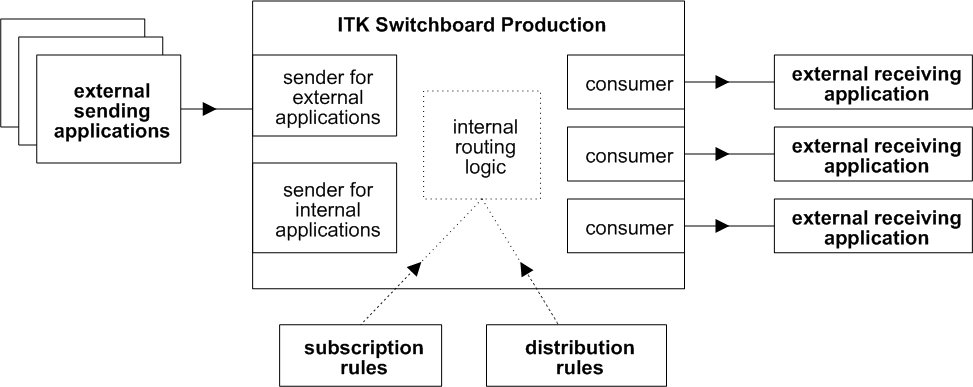
The production includes two kinds of Ensemble business hosts:
-
ITK listeners. Each listener is a business service that receives SOAP messages from sending applications. Typically the ITK Switchboard contains two listeners: one to handle applications that are external to the production, and another one to handle messages that originate within the production.
Each listener uses a single port and has a single security policy.
-
ITK consumers. Each consumer is a business operation that sends SOAP messages to one external application.
The ITK Switchboard uses the generic term systems or applications to refer collectively to external systems. When you configure the ITK Switchboard, you declare all systems that the Switchboard will use. Note that some systems can both send and receive messages from the switchboard. This means that, for some systems, the production contains both a corresponding listener and a corresponding consumer.
The ITK Switchboard production provides internal, data-driven logic to route messages; the production does not use a business host for this purpose. The routing logic uses the subscription and distribution rules that you define when you configure the Switchboard.
The listeners and consumers communicate via SOAP with the external systems as follows:
-
The SOAP messages follow the Web Services-Addressing (WS-Addressing) and Web Service-Security (WS-Security) standards.
WS-Addressing header elements indicate the UUID of the message, the corresponding SOAP action, the sender of the message, and confirmation of the designated recipient of the message.
WS-Security header elements include a signed timestamp (with expiry). The Switchboard can then use the public key of the sending application to ensure that the message is genuine. It is also possible to sign and encrypt the entire SOAP body.
SSL/TLS is also available.
-
The SOAP body can have any content. The content is matched against the SOAP action.
You configure the Switchboard to expect specific SOAP actions in specific contexts. The Switchboard uses the following system to handle the wide variety of messages that it routes:
-
The Switchboard provides a set of services that match the UK NHS CfH ITK Services. This book uses the phrase ITK service, to distinguish these from web services and from business services.
Each ITK service corresponds to a SOAP action.
Each ITK service has a short service name, for use within the Switchboard. It also has a behavior type, which indicates what behavior is expected in response to the inbound request. Also, an ITK service uses specific request and response message classes.
-
When you configure listeners, you indicate the ITK services that each listener will use.
-
When you configure consumers, you indicate the ITK services that each consumer will use.
-
When you define subscription rules and distribution rules, you indicate the ITK services used in each rule.
Getting Started
To start to create the ITK Switchboard production:
-
Use the Management Portal to create a new Ensemble-enabled namespace.
-
Access the following web page:
http://localhost:57772/csp/itk/EnsLib.ITK.Setup.UI.RegistryViewer.clsWhere localhost is the server on which Ensemble is running, 57772 is the web server port that Ensemble is using, and itk is the namespace that you created.
This page is a specialized version of the standard Ensemble production configuration page. Two buttons at the top let you control whether you are viewing senders or consumers:

Click this to view systems, senders, and listeners. 
Click this to view consumers, subscription rules, and distribution rules. -
Click New.
-
Specify the following information:
-
Package Name — Package to contain the production class.
-
Production Name — Name of the production class.
-
Production Description — Optional description of the production.
-
-
Click OK.
Defining ITK Services
As noted earlier, the Switchboard provides a set of ITK services that match the UK NHS CfH ITK Services. Obtain the configuration data for these services from the InterSystems Worldwide Response Center (WRC)Opens in a new tab and load it into Ensemble as directed.
Normally you would not edit this data; if you do, your solution might no longer be ITK-compliant. If you do edit this data, specify the following details for each ITK service:
Required. Unique, internal name of the ITK service, usually a short name. You may find it convenient to use a short form of the SOAP action. For example: ConfirmMessageReceipt-v1-0
Required. Unique SOAP action. For example: urn:nhs-itk:201005:ConfirmMessageReceipt-v1-0
Required. Select one of the following:
-
Request-Response — The sender sends a request and receives a response that contains the requested information.
The response can be synchronous or asynchronous.
-
Post — The sender sends a request and receives a simple OK response. The sender is essentially treating this as a fire and forget operation. Note the sender may be a sending application into the switchboard or the switchboard itself sending a message to a consuming application.
-
Acknowledged — Similar to Post, but includes asynchronous technical and business acknowledgements.
-
Queue Collection — The sender sends the messages to a queue and the consumer picks up the messages later rather than in real time. This behavior type is useful for a consumer associated with an application that has intermittent network connectivity. An example is applications running on handheld devices.
-
Fault Handler — A service used to receive asynchronous faults.
-
Asynch Response Handler — A service used to receive asynchronous responses.
The Switchboard automatically mediates the handling of synchronous and asynchronous communications.
Do not change the value for this.
Do not change the value for this.
Do not change the value for this.
Do not change the value for this.
Defining Systems
To define each system, display the basic Switchboard production and then do the following:
-
Click the View Senders button
 .
. -
Click the plus sign + next to Systems.
-
Specify the following details:
ApplicationNameRequired. Unique name of the system.
Each system can have an associated consumer, a listener or both. See below for information on choosing suitable names in these cases.
ApplicationRouterSpecify the name of a business rule in Ensemble that contains the rules that map the content of the message to consumers for content-based routing.
-
Click OK.
System Names for Consumers
If the system represents a consumer, the reconciliation process examines the routing rules and creates the needed business operation for that system. The name of the system becomes the name of a business operation.
For pure consumers, the name of the system is not that important and is only used internally. However, note that if the same system uses the queue collection facility (that is, sends requests to get the messages) or it if responds asynchronously (that is, sends responses) then the system is also a listener; see the next heading.
System Names for Listeners
The ITK Switchboard has a limited amount of business services that vary by port numbers and security configurations. It is common to have one business service for internal systems and another for external systems.
For a listener, the name of the system must match the ‘From’ value in the SOAP Header. This allows more than one system to send messages into the same business service, while enabling the Switchboard to route the messages easily based on the sending system.
Defining the Listeners
To define each listener, display the basic Switchboard production and then do the following:
-
Click the View Senders button
 .
. -
Click the plus sign + next to Listeners.
-
Specify a name for the listener, which is a business service.
-
Click OK.
-
Click the circle for a sender that sends to this listener.
With the left mouse down, drag a line from this to the listener.
When you do so, Ensemble displays a dialog box where you can specify configuration details.
-
For each service expected from this sender, do the following:
-
Select a service from the Web Service drop-down list.
-
Select a value for Invocation Pattern, one of the following:
-
Asynchronous
-
Synchronous
-
Derived
This option matters only if the service is a request/response type.
-
-
Ignore Validate Payload. This option is for future use.
-
Click Save.
-
-
When you are done specifying services, click OK.
Defining the Consumers
To define consumers, display the basic Switchboard production and then do the following:
-
Click the View Consumers button
 .
. -
Click the plus sign + next to Consumers.
-
For ApplicationName, specify a consumer name.
-
Click OK.
Make sure that the new consumer is selected.
-
On the Settings tab, expand the Consumer Settings section.
-
Click the search button next to Services.
-
For each service expected from this sender, do the following:
-
Select a service from the Web Service drop-down list.
-
Select a value for Invocation Pattern, one of the following:
-
Asynchronous
-
Synchronous
This option matters only if the service is a request/response type.
-
-
For Partial Logical Endpoint, specify a logical path to append to the base endpoint of the web service used by this consumer. The base endpoint is configured (later) in the business operation.
-
For Partial Physical Endpoint, specify an optional physical path to append to the base endpoint, which is configured (later) in the business operation.
-
Click Save.
-
-
When you are done specifying services, click OK.
Defining Subscription Rules
A subscription rule sends all messages for given service from a given sender to a specific consumer.
To define subscription rules, display the basic Switchboard production and then do the following:
-
Click the View Consumers button
 .
. -
Click the circle for a sender that sends to this consumer.
With the left mouse down, drag a line from this to the consumer.
When you do so, Ensemble displays a dialog box where you can specify configuration details for the subscription rule.
-
Select a service and click OK.
Currently it is an error to set up more than one subscriber for a request/response service from the same application.
Defining Distribution Rules
A distribution rule applies to requests that are wrapped in a distribution envelope, which can contain logical addresses. A distribution rule describes how to dispatch the payload to the systems specified by the addresses.
To define distribution rules, display the basic Switchboard production and then do the following:
-
Click the View Consumers button
 .
. -
Select a consumer.
-
On the Settings tab, expand the Consumer Settings section.
-
Click the search button next to DistributionRules.
-
For each distribution rule for this consumer, do the following:
-
Select a service from the Web Service drop-down list.
-
Select a value for Distribution Mode, one of the following:
-
Authoritative
-
Non-Authoritative
This option refers to the mode needed for the distribution rule to be effective. The distribution mode is set by the business service.
Authoritative means that the Switchboard should deliver this service to this component only if we are acting authoritatively. The best way to look at this is to think about the ITK Switchboard at the edge of a data center. We might for example communicate with external systems outside of our data center, but we should only communicate with these external systems when processing a message from one of our internal systems (we call this authoritatively).
In contrast, if we receive a message from one of the external systems we may expect that this external system has already spoken to any other external systems. In such a case, we should not relay the message on (i.e. we would not send the message on to these systems when we are acting non-authoritatively).
-
-
For Logical Address, specify an address inside the distribution envelope of a SOAP message.
-
Click Save.
-
-
When you are done specifying rules, click OK.
Reconciling the ITK Switchboard Production
The reconciliation process examines the routing rules and creates any needed business services and business operations.
To reconcile the production, display the production configuration in the Management Portal and click the Reconcile button.
Completing the Configuration of the ITK Switchboard Production
After performing reconciliation, complete the configuration by specifying settings for the business services and business operations.
Configuring the Business Services (Listeners)
Each listener is an instance of EnsLib.ITK.Framework.Service.SOAPRequestHandlerOpens in a new tab and uses the adapter class EnsLib.SOAP.InboundAdapterOpens in a new tab.
For each listener, specify the following settings:
Specify the same value that is in the To element in the SOAP header, for SOAP messages received by this business service.
This setting applies only when processing address inside an incoming distribution envelope using distribution rules. If the service receives from internal applications, use the value authoritatively. If the service receives from external applications, use the value non-authoritatively.
Vocabulary to use for faults. For ITK, use the value 2.16.840.1.113883.2.1.3.2.4.17.268
Password for the user. Ensure that the caller is a registered Caché user.
Indicates which parts of the header are expected to be signed by the digital signature provided.
Turn on if this service should check the body is encrypted. Useful if receiving from an external system over unsecure connection. Typically do not encrypt the messages.
Specify ITKMEssageRouter
Specify the port number on which Ensemble should listen.
Specify other settings as wanted; see other Ensemble documentation.
Configuring the Business Operations (Consumers)
Each consumer is an instance of EnsLib.ITK.Framework.Operation.SOAPOperationOpens in a new tab and uses the adapter class EnsLib.SOAP.OutboundAdapterOpens in a new tab.
For each consumer, specify the following settings:
Specify the base logical endpoint for the web service. The actual endpoint is this endpoint plus the partial logical endpoint specified in the consumer registry.
Name of the sending application, typically the name of the consumer.
If you are not signing the messages (see the Sign Headers setting), then specify the username to place in the username field in the outbound messages.
Vocabulary to use for faults. For ITK, use the value 2.16.840.1.113883.2.1.3.2.4.17.268
Set this to true.
Specifies an optional throttle on the business operation. This value is the time in seconds between requests.
The standard ITK signing level is 2, which signs the timestamp. In a trusted environment, you can use 0, which means that the messages do not need to be signed. Use higher values if needed; for details, see the tooltip for this setting.
The username in a pre-installed X509 certificate with which to sign the request. Load this certificate into Caché as described in the chapter “Setup and Other Common Activities” in Securing Caché Web Services.
If you want to encrypt the request body, then determines if this is 128–bit or 256–bit encryption. Keep None for no encryption.
Same as X509CertificationSign but for the encryption. If used typically the same as signing certificate. Do not encrypt unless there is a good reason to do so.
Set to true if this consumer will call in at a time of its choosing to collect the messages. In this case, the business operation saves the message away.
Specifies the maximum number of messages that the consumer can subsequently request if using subscription pull. Specify –1 for no limit.
Specify other settings as wanted; see other Ensemble documentation.